Month: July 2016

Implementing Undirected Graphs in Python

Anirudh Technical , , , , , , ,

There are 2 popular ways of representing an undirected graph.

Adjacency List
Each list describes the set of neighbors of a vertex in the graph.

adjacencyList

Adjacency Matrix
The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.

adjacencyMatrix

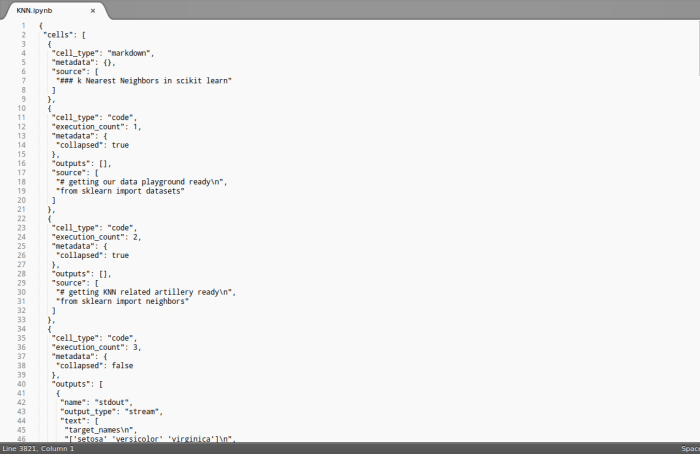
Here’s an implementation of the above in Python:

class Vertex:
def __init__(self, vertex):
self.name = vertex
self.neighbors = []
def add_neighbor(self, neighbor):
if isinstance(neighbor, Vertex):
if neighbor.name not in self.neighbors:
self.neighbors.append(neighbor.name)
neighbor.neighbors.append(self.name)
self.neighbors = sorted(self.neighbors)
neighbor.neighbors = sorted(neighbor.neighbors)
else:
return False
def add_neighbors(self, neighbors):
for neighbor in neighbors:
if isinstance(neighbor, Vertex):
if neighbor.name not in self.neighbors:
self.neighbors.append(neighbor.name)
neighbor.neighbors.append(self.name)
self.neighbors = sorted(self.neighbors)
neighbor.neighbors = sorted(neighbor.neighbors)
else:
return False
def __repr__(self):
return str(self.neighbors)
class Graph:
def __init__(self):
self.vertices = {}
def add_vertex(self, vertex):
if isinstance(vertex, Vertex):
self.vertices[vertex.name] = vertex.neighbors
def add_vertices(self, vertices):
for vertex in vertices:
if isinstance(vertex, Vertex):
self.vertices[vertex.name] = vertex.neighbors
def add_edge(self, vertex_from, vertex_to):
if isinstance(vertex_from, Vertex) and isinstance(vertex_to, Vertex):
vertex_from.add_neighbor(vertex_to)
if isinstance(vertex_from, Vertex) and isinstance(vertex_to, Vertex):
self.vertices[vertex_from.name] = vertex_from.neighbors
self.vertices[vertex_to.name] = vertex_to.neighbors
def add_edges(self, edges):
for edge in edges:
self.add_edge(edge[0],edge[1])
def adjacencyList(self):
if len(self.vertices) >= 1:
return [str(key) + ":" + str(self.vertices[key]) for key in self.vertices.keys()]
else:
return dict()
def adjacencyMatrix(self):
if len(self.vertices) >= 1:
self.vertex_names = sorted(g.vertices.keys())
self.vertex_indices = dict(zip(self.vertex_names, range(len(self.vertex_names))))
import numpy as np
self.adjacency_matrix = np.zeros(shape=(len(self.vertices),len(self.vertices)))
for i in range(len(self.vertex_names)):
for j in range(i, len(self.vertices)):
for el in g.vertices[self.vertex_names[i]]:
j = g.vertex_indices[el]
self.adjacency_matrix[i,j] = 1
return self.adjacency_matrix
else:
return dict()
def graph(g):
""" Function to print a graph as adjacency list and adjacency matrix. """
return str(g.adjacencyList()) + '\n' + '\n' + str(g.adjacencyMatrix())
###################################################################################
a = Vertex('A')
b = Vertex('B')
c = Vertex('C')
d = Vertex('D')
e = Vertex('E')
a.add_neighbors([b,c,e])
b.add_neighbors([a,c])
c.add_neighbors([b,d,a,e])
d.add_neighbor(c)
e.add_neighbors([a,c])
g = Graph()
print(graph(g))
print()
g.add_vertices([a,b,c,d,e])
g.add_edge(b,d)
print(graph(g))
view raw graphUndirected.py hosted with ❤ by GitHub

Output:

{}
{}
["A:['B', 'C', 'E']", "C:['A', 'B', 'D', 'E']", "B:['A', 'C', 'D']", "E:['A', 'C']", "D:['B', 'C']"]
[[ 0. 1. 1. 0. 1.]
[ 1. 0. 1. 1. 0.]
[ 1. 1. 0. 1. 1.]
[ 0. 1. 1. 0. 0.]
[ 1. 0. 1. 0. 0.]]
view raw graphUndirected_output.txt hosted with ❤ by GitHub

Deterministic Selection Algorithm Python Code

Anirudh Technical , , , , , , ,

Through this post, I’m sharing Python code implementing the median of medians algorithm, an algorithm that resembles quickselect, differing only in the way in which the pivot is chosen, i.e, deterministically, instead of at random.

Its best case complexity is O(n) and worst case complexity O(nlog2n)

I don’t have a formal education in CS, and came across this algorithm while going through Tim Roughgarden’s Coursera MOOC on the design and analysis of algorithms. Check out my implementation in Python.

def merge_tuple(a,b):
""" Function to merge two arrays of tuples """
c = []
while len(a) != 0 and len(b) != 0:
if a[0][0] < b[0][0]:
c.append(a[0])
a.remove(a[0])
else:
c.append(b[0])
b.remove(b[0])
if len(a) == 0:
c += b
else:
c += a
return c
def mergesort_tuple(x):
""" Function to sort an array using merge sort algorithm """
if len(x) == 0 or len(x) == 1:
return x
else:
middle = len(x)/2
a = mergesort_tuple(x[:middle])
b = mergesort_tuple(x[middle:])
return merge_tuple(a,b)
def lol(x,k):
""" Function to divide a list into a list of lists of size k each. """
return [x[i:i+k] for i in range(0,len(x),k)]
def preprocess(x):
""" Function to assign an index to each element of a list of integers, outputting a list of tuples"""
return zip(x,range(len(x)))
def partition(x, pivot_index = 0):
""" Function to partition an unsorted array around a pivot"""
i = 0
if pivot_index !=0: x[0],x[pivot_index] = x[pivot_index],x[0]
for j in range(len(x)-1):
if x[j+1] < x[0]:
x[j+1],x[i+1] = x[i+1],x[j+1]
i += 1
x[0],x[i] = x[i],x[0]
return x,i
def ChoosePivot(x):
""" Function to choose pivot element of an unsorted array using 'Median of Medians' method. """
if len(x) <= 5:
return mergesort_tuple(x)[middle_index(x)]
else:
lst = lol(x,5)
lst = [mergesort_tuple(el) for el in lst]
C = [el[middle_index(el)] for el in lst]
return ChoosePivot(C)
def DSelect(x,k):
""" Function to """
if len(x) == 1:
return x[0]
else:
xpart = partition(x,ChoosePivot(preprocess(x))[1])
x = xpart[0] # partitioned array
j = xpart[1] # pivot index
if j == k:
return x[j]
elif j > k:
return DSelect(x[:j],k)
else:
k = k - j - 1
return DSelect(x[(j+1):], k)
arr = range(100,0,-1)
print DSelect(arr,50)
%timeit DSelect(arr,50)
view raw DSelect.py hosted with ❤ by GitHub

I get the following output:

51
100 loops, best of 3: 2.38 ms per loop

Note that on the same input, quickselect is faster, giving us:

1000 loops, best of 3: 254 µs per loop

scikit-learn Linear Regression Example

Anirudh Technical , , , , , , , , , ,

Here’s a quick example case for implementing one of the simplest of learning algorithms in any machine learning toolbox – Linear Regression. You can download the IPython / Jupyter notebook here so as to play around with the code and try things out yourself.

I’m doing a series of posts on scikit-learn. Its documentation is vast, so unless you’re willing to search for a needle in a haystack, you’re better off NOT jumping into the documentation right away. Instead, knowing chunks of code that do the job might help.

Loading
Sorry, something went wrong. Reload?
Sorry, we cannot display this file.
Sorry, this file is invalid so it cannot be displayed.
view raw linear_regression.ipynb hosted with ❤ by GitHub

Sharing IPython / Jupyter Notebooks via WordPress

Anirudh Technical , ,

In order to share (a static version of) your IPython / Jupyter notebook on your WordPress site, follow three straightforward steps.

Step 1: Let’s say your Jupyter Notebook looks like this:

blog_item_20160718_01

Open this notebook in a text editor and copy the content which may look like so:

blog_item_20160718_02

Step 2: Ctrl + A and Ctrl + C this content. Then Ctrl + V this to a GitHub Gist that you should create, like so:

blog_item_20160718_03

Step 3: Now simply Create public gist and embed the gist like you always embed gists on WordPress, viz., go to the HTML editor and add like so:

blog_item_20160718_04

I followed the exact steps that I’ve mentioned above to get the following result:

Loading
Sorry, something went wrong. Reload?
Sorry, we cannot display this file.
Sorry, this file is invalid so it cannot be displayed.
view raw knn.ipynb hosted with ❤ by GitHub

 

Randomized Selection Algorithm (Quickselect) – Python Code

Anirudh Technical , , ,

Find the kth smallest element in an array without sorting.

That’s basically what this algorithm does. It piggybacks on the partition subroutine from the Quick Sort. If you don’t know what that is, you can check out more about the Quick Sort algorithm here and here, and understand the usefulness of partitioning an unsorted array around a pivot.

Selecting_quickselect_frames
Animated visualization of the randomized selection algorithm selecting the 22nd
 smallest value

Python Implementation

from random import randrange
def partition(x, pivot_index = 0):
i = 0
if pivot_index !=0: x[0],x[pivot_index] = x[pivot_index],x[0]
for j in range(len(x)-1):
if x[j+1] < x[0]:
x[j+1],x[i+1] = x[i+1],x[j+1]
i += 1
x[0],x[i] = x[i],x[0]
return x,i
def RSelect(x,k):
if len(x) == 1:
return x[0]
else:
xpart = partition(x,randrange(len(x)))
x = xpart[0] # partitioned array
j = xpart[1] # pivot index
if j == k:
return x[j]
elif j > k:
return RSelect(x[:j],k)
else:
k = k - j - 1
return RSelect(x[(j+1):], k)
x = [3,1,8,4,7,9]
for i in range(len(x)):
print RSelect(x,i),
view raw RSelect.py hosted with ❤ by GitHub

 

Related Posts
Quick Sort Python Code
Computing Work Done (Total Pivot Comparisons) by Quick Sort

Computing Work Done (Total Pivot Comparisons) by Quick Sort

Anirudh Technical , , , , ,

A key aspect of the Quick Sort algorithm is how the pivot element is chosen. In my earlier post on the Python code for Quick Sort, my implementation takes the first element of the unsorted array as the pivot element.

However with some mathematical analysis it can be seen that such an implementation is O(n2) in complexity while if a pivot is randomly chosen, the Quick Sort algorithm is O(nlog2n).

To witness this in action, one can measure the work done by the algorithm comparing two cases, one with a randomized pivot choice – and one with a fixed pivot choice, say the first element of the array (or the last element of the array).

Implementation

A decent proxy for the amount of work done by the algorithm would be the number of pivot comparisons. These comparisons needn’t be computed one-by-one, rather when there is a recursive call on a subarray of length m, you should simply add m−1 to your running total of comparisons.

3 Cases

To put things in perspective, let’s look at 3 cases. (This is basically straight out of a homework assignment from Tim Roughgarden’s course on the Design and Analysis of Algorithms).
Case I with the pivot being the first element.
Case II with the pivot being the last element.
Case III using the “median-of-three” pivot rule. The primary motivation behind this rule is to do a little bit of extra work to get much better performance on input arrays that are nearly sorted or reverse sorted.

Median-of-Three Pivot Rule

Consider the first, middle, and final elements of the given array. (If the array has odd length it should be clear what the “middle” element is; for an array with even length 2k, use the kth element as the “middle” element. So for the array 4 5 6 7, the “middle” element is the second one —- 5 and not 6! Identify which of these three elements is the median (i.e., the one whose value is in between the other two), and use this as your pivot.

Python Code

This file contains all of the integers between 1 and 10,000 (inclusive, with no repeats) in unsorted order. The integer in the ith row of the file gives you the ith entry of an input array. I downloaded this file and named it QuickSort_List.txt

You can run the code below and see for yourself that the number of comparisons for Case III are 138,382 compared to 162,085 and 164,123 for Case I and Case II respectively. You can play around with the code in an IPython / Jupyter notebook here.

#!/usr/bin/env
# Case I
# First element of the unsorted array is chosen as pivot element for sorting using Quick Sort
def countComparisonsWithFirst(x):
""" Counts number of comparisons while using Quick Sort with first element of unsorted array as pivot """
global count_pivot_first
if len(x) == 1 or len(x) == 0:
return x
else:
count_pivot_first += len(x)-1
i = 0
for j in range(len(x)-1):
if x[j+1] < x[0]:
x[j+1],x[i+1] = x[i+1], x[j+1]
i += 1
x[0],x[i] = x[i],x[0]
first_part = countComparisonsWithFirst(x[:i])
second_part = countComparisonsWithFirst(x[i+1:])
first_part.append(x[i])
return first_part + second_part
# Case II
# Last element of the unsorted array is chosen as pivot element for sorting using Quick Sort
def countComparisonsWithLast(x):
""" Counts number of comparisons while using Quick Sort with last element of unsorted array as pivot """
global count_pivot_last
if len(x) == 1 or len(x) == 0:
return x
else:
count_pivot_last += len(x)-1
x[0],x[-1] = x[-1],x[0]
i = 0
for j in range(len(x)-1):
if x[j+1] < x[0]:
x[j+1],x[i+1] = x[i+1], x[j+1]
i += 1
x[0],x[i] = x[i],x[0]
first_part = countComparisonsWithLast(x[:i])
second_part = countComparisonsWithLast(x[i+1:])
first_part.append(x[i])
return first_part + second_part
# Case III
# Median-of-three method used to choose pivot element for sorting using Quick Sort
def middle_index(x):
""" Returns the index of the middle element of an array """
if len(x) % 2 == 0:
middle_index = len(x)/2 - 1
else:
middle_index = len(x)/2
return middle_index
def median_index(x,i,j,k):
""" Returns the median index of three when passed an array and indices of any 3 elements of that array """
if (x[i]-x[j])*(x[i]-x[k]) < 0:
return i
elif (x[j]-x[i])*(x[j]-x[k]) < 0:
return j
else:
return k
def countComparisonsMedianOfThree(x):
""" Counts number of comparisons while using Quick Sort with median-of-three element is chosen as pivot """
global count_pivot_median
if len(x) == 1 or len(x) == 0:
return x
else:
count_pivot_median += len(x)-1
k = median_index(x, 0, middle_index(x), -1)
if k != 0: x[0], x[k] = x[k], x[0]
i = 0
for j in range(len(x)-1):
if x[j+1] < x[0]:
x[j+1],x[i+1] = x[i+1], x[j+1]
i += 1
x[0],x[i] = x[i],x[0]
first_part = countComparisonsMedianOfThree(x[:i])
second_part = countComparisonsMedianOfThree(x[i+1:])
first_part.append(x[i])
return first_part + second_part
#####################################################################
# initializing counts
count_pivot_first = 0; count_pivot_last = 0; count_pivot_median = 0
#####################################################################
# Cast I
# Read the contents of the file into a Python list
NUMLIST_FILENAME = "QuickSort_List.txt"
inFile = open(NUMLIST_FILENAME, 'r')
with inFile as f: numList = [int(integers.strip()) for integers in f.readlines()]
# call functions to count comparisons
countComparisonsWithFirst(numList)
#####################################################################
# Read the contents of the file into a Python list
NUMLIST_FILENAME = "QuickSort_List.txt"
inFile = open(NUMLIST_FILENAME, 'r')
with inFile as f: numList = [int(integers.strip()) for integers in f.readlines()]
# call functions to count comparisons
countComparisonsWithLast(numList)
#####################################################################
# Read the contents of the file into a Python list
NUMLIST_FILENAME = "QuickSort_List.txt"
inFile = open(NUMLIST_FILENAME, 'r')
with inFile as f: numList = [int(integers.strip()) for integers in f.readlines()]
# call functions to count comparisons
countComparisonsMedianOfThree(numList)
#####################################################################
print count_pivot_first, count_pivot_last, count_pivot_median
view raw countComparisons.py hosted with ❤ by GitHub

Quick Sort Python Code

Anirudh Technical , , ,

Sorting_quicksort_anim

Yet another post for the crawlers to better index my site for algorithms and as a repository for Python code. The quick sort algorithm is well explained in the topmost Google search result for ‘Quick Sort Python Code’, but the code is unnecessarily convoluted. Instead, go with the code below.

In it, I assume the pivot to be the first element. You can easily add a function to  randomize selection of the pivot. Choosing a random pivot minimizes the chance that you will encounter worst-case O(n2) performance. Always choosing first or last would cause worst-case performance for nearly-sorted or nearly-reverse-sorted data.

def quicksort(x):
if len(x) == 1 or len(x) == 0:
return x
else:
pivot = x[0]
i = 0
for j in range(len(x)-1):
if x[j+1] < pivot:
x[j+1],x[i+1] = x[i+1], x[j+1]
i += 1
x[0],x[i] = x[i],x[0]
first_part = quicksort(x[:i])
second_part = quicksort(x[i+1:])
first_part.append(x[i])
return first_part + second_part
alist = [54,26,93,17,77,31,44,55,20]
quicksort(alist)
print(alist)
view raw quicksort.py hosted with ❤ by GitHub

Also read:
Computing Work Done (Total Pivot Comparisons) by Quick Sort
Karatsuba Multiplication Algorithm – Python Code
Merge Sort