Motivation for this blog post
I’ve enrolled in Stanford Professor Tim Roughgarden’s Coursera MOOC on the design and analysis of algorithms, and while he covers the theory and intuition behind the algorithms in a surprising amount of detail, we’re left to implement them in a programming language of our choice.
And I’m ging to post Python code for all the algorithms covered during the course!
The Karatsuba Multiplication Algorithm
Karatsuba’s algorithm reduces the multiplication of two n-digit numbers to at most 
single-digit multiplications in general (and exactly 
when n is a power of 2). Although the familiar grade school algorithm for multiplying numbers is how we work through multiplication in our day-to-day lives, it’s slower (
) in comparison, but only on a computer, of course!
Here’s how the grade school algorithm looks:
(The following slides have been taken from Tim Roughgarden’s notes. They serve as a good illustration. I hope he doesn’t mind my sharing them.)
…and this is how Karatsuba Multiplication works on the same problem:
A More General Treatment
Let 
and 
be represented as 
-digit strings in some base 
. For any positive integer 
less than , one can write the two given numbers as
,
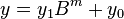where 
and 
are less than 
. The product is then
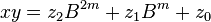
where
These formulae require four multiplications, and were known to Charles Babbage. Karatsuba observed that 
can be computed in only three multiplications, at the cost of a few extra additions. With 
and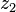 
as before we can calculate
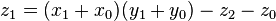
which holds since
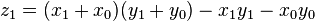
A more efficient implementation of Karatsuba multiplication can be set as 
, where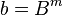 
.
Example
To compute the product of 12345 and 6789, choose B = 10 and m = 3. Then we decompose the input operands using the resulting base (Bm = 1000), as:
- 12345 = 12 · 1000 + 345
- 6789 = 6 · 1000 + 789
Only three multiplications, which operate on smaller integers, are used to compute three partial results:
- z2 = 12 × 6 = 72
- z0 = 345 × 789 = 272205
- z1 = (12 + 345) × (6 + 789) − z2 − z0 = 357 × 795 − 72 − 272205 = 283815 − 72 − 272205 = 11538
We get the result by just adding these three partial results, shifted accordingly (and then taking carries into account by decomposing these three inputs in base 1000 like for the input operands):
- result = z2 · B2m + z1 · Bm + z0, i.e.
- result = 72 · 10002 + 11538 · 1000 + 272205 = 83810205.
Pseudocode and Python code
| procedure karatsuba(num1, num2) | |
| if (num1 < 10) or (num2 < 10) | |
| return num1*num2 | |
| /* calculates the size of the numbers */ | |
| m = max(size_base10(num1), size_base10(num2)) | |
| m2 = m/2 | |
| /* split the digit sequences about the middle */ | |
| high1, low1 = split_at(num1, m2) | |
| high2, low2 = split_at(num2, m2) | |
| /* 3 calls made to numbers approximately half the size */ | |
| z0 = karatsuba(low1,low2) | |
| z1 = karatsuba((low1+high1),(low2+high2)) | |
| z2 = karatsuba(high1,high2) | |
| return (z2*10^(2*m2))+((z1-z2-z0)*10^(m2))+(z0) |
| def karatsuba(x,y): | |
| """Function to multiply 2 numbers in a more efficient manner than the grade school algorithm""" | |
| if len(str(x)) == 1 or len(str(y)) == 1: | |
| return x*y | |
| else: | |
| n = max(len(str(x)),len(str(y))) | |
| nby2 = n / 2 | |
| a = x / 10**(nby2) | |
| b = x % 10**(nby2) | |
| c = y / 10**(nby2) | |
| d = y % 10**(nby2) | |
| ac = karatsuba(a,c) | |
| bd = karatsuba(b,d) | |
| ad_plus_bc = karatsuba(a+b,c+d) - ac - bd | |
| # this little trick, writing n as 2*nby2 takes care of both even and odd n | |
| prod = ac * 10**(2*nby2) + (ad_plus_bc * 10**nby2) + bd | |
| return prod |
Hi, things like getting input as integers and using functions may be a trouble for beginners, so here is a “running off the shelf” version: https://repl.it/CBno
LikeLike
Thank you so much for the “writing n as 2*nby2” tip. Without it, just using 10**n * (a * c), the algorithm works for all four-digit numbers (as far as I can tell), but fails on about one eight-digit problem out of eight, more with higher numbers of digits. I had found that the failures were related to getting an odd number of digits with a split, since leading zeros are dropped (45670123 splits as 4567 and 123), and had been trying to fix it by going to strings and padding out leading zeros. That actually reduced the failure rate, but fails still occurred. Your simple fix removed the whole issue!
LikeLike
Hi,
I found your implementation amusing because of the usage of / and % operators as they take more time than the actual problem
Did you test your results for large size inputs?
I believe those operators should be replaced by string concatenation for an efficient implementation
LikeLiked by 1 person
Hi, thanks for the 2*nby2 tip! However i’m a noob and still don’t understand how it works. Is it because python remembers that for odd numbers, the nby2 is actually a float and accounts for that when doing the multiplication?
Thanks!
LikeLike
Didn’t work for me! I copy-pasted verbatim and got RecursionError, maximum recursion depth exceeded with getting the str of an object.
LikeLike
I wanted to read your whole code, but the starting of the code has the biggest flaw.
if len(str(x)) == 1 or len(str(y)) == 1:
return x*y
what if x is 10, and y is 1 you still cant do 101.. you have to 1001 recursively.
Unnecessary use of ** and %. Do you know ** works internally?
LikeLike
“your program should restrict itself to multiplying only pairs of single-digit numbers.”
with that IF statement you are failing to do so… lets say you multiply 7 x 213213321….(large number). Your code will do directly the multiplication without using the recursive method. (That multiplication will be done by whatever implementation python uses … perhaps its karatsuba too :D)
What you can do is (lets say x has 1 digit and y has >1 digit):
– check that we are in that case
– you cannot split x, so you have to split y: 1 part with all digits but last one, and 2nd part with last digit
– set a to 0 so you can use your f(a,b,c,d) katsuba formula when a is 0. if the 1 digit number is y, then c=0.
– do this recursively until you arrive to 1digit by 1digit number multiplications
Btw your code fails, has recursion errors. You shouldnt split numbers by half of the max(len(x),len(y)). what happens if x=123 and y=12345678… how do you split x into 4 digits?…you should use min instead of max. so you split x into [1,23] and y [123456,78] (or [12,3] and y [1234568,8]
LikeLike
Thank you for the python code. This will help me multiply big numbers in short time.
LikeLike
This is my first time visit here. From the tons of comments on your articles.I guess I am not only one having all the enjoyment right here! ExcelR Data Science Courses
LikeLike
I do not know why I got a wrong result when I have reproduced the code on my test case, it fails, anyone knows where the problem is?
LikeLike
[…] Offer […]
LikeLike
[…] Supply […]
LikeLike
[…] Source […]
LikeLike
BBQ Grill/Fire Pit in 2001 Years, Our Factory Can Provide Cheap Price and Good Quality Product Around the World, Currently, Main Market is Germany/Poland/UK/US, Quality Inspection Standard is in Accordance with France/Germany. Our products look so cool and have hundreds of styles and sizes for you to choose. In this way, you can meet different requirements in different places. I believe there will be styles that you love!
LikeLike
Thank you for the code. I was able to build this website using python.
LikeLike
Hi waht should be the implementation of karatsuba for base 2 or any other base?
LikeLike
The code need some modification to used // instead of /
LikeLike
Thank you for the great tips. also learn Data Science Course in Jersey City using python and r programming.
LikeLike
thank you for the python code ..
Certification Course on
Data Science in London
LikeLike